Grafting
A complex projective structure on a surface S is a structure locally modeled on CP^1. In terms of (G,X)-structure, this is a (PSL(2,C), CP^1)-structure on S. For example, a Fuchsian uniformization gives a complex projective structure.
If S has a complex projective structure, by analytic continuation of the local structure, we obtain an equivariant map from the universal cover of S to CP^1. In general, it is known that a (G,X)-structure defines a developing map and we can recover the (G,X)-structure from the developing map conversely.
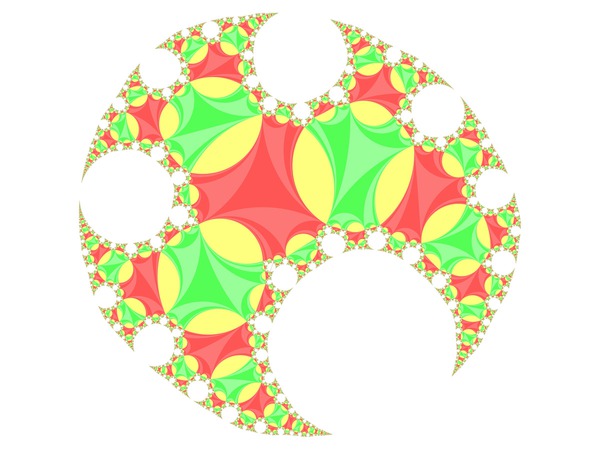
We can construct a complex projective structure from a Fuchsian uniformization by inserting annulus along a simple closed curve on S. This operation is called the grafting. The left of the pictures below describes the universal cover of a genus 2 hyperbolic surface.
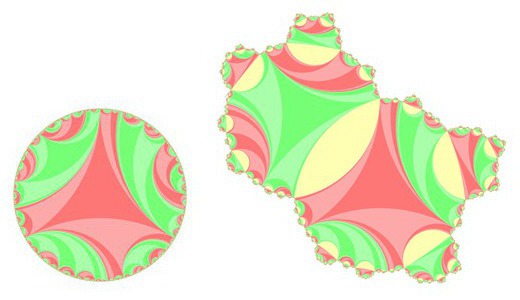
The right is the developed image of the grafted surface. You can see that the right picture is obtained from the left grafting yellow strips. These yellow strips are the lifts of the grafted annulus. The following is a continuous family of graftings obtained by a complex earthquake deformation. (To see larger one (about 3.4MB), click the image.)
The grafting along a simple closed curve can be easily generalized for multi-curves. (Moreover, we can extend the grafting operation for measured laminations on S.) The following is the developed image of a complex projective structure on a genus 2 surface. This is obtained from a Fuchsian surface of genus 2 grafting along a maximal multi-curve system. I put the picture of the corresponding bending surface developed in the upper half space. (Click the images if you want to see higher resolution ones, about 500KB and 2MB respectively.)